指数移動平均(EMA)

指数移動平均(Exponentially Moving Average : EMA)とは、指数関数的に直近の値にウェイトを置いた平均値のこと。

指数平滑移動平均(Exponentially Smoothed Moving Average ： ESMA)、指数加重移動平均 (Exponentially Weighted Moving Average ： EWMA)ともいう。

単純移動平均は「過去の価格も現在の価格と同様の重みで計算される」ことが弱点とされる。この弱点を補う為に考えられたのがこの指数移動平均である。
※同様のコンセプトで加重移動平均(WMA)がある。

指数移動平均の値を時系列で並べ、それを線で繋げたものを指数移動平均線といい、トレンドの方向を見る指標として使う。
※ 基本的な使い方は単純移動平均と同様。（単純移動平均の説明ページを参照）

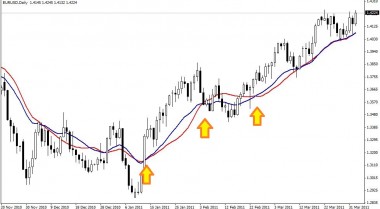
赤い線が単純移動平均、青い線が指数移動平均である。（両方とも20日）

価格の上昇／下降に対する反応が指数移動平均の方が早く出る。（矢印で示す箇所で指数移動平均が単純移動平均を追い越してる）

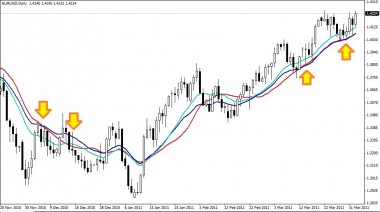
赤い線が単純移動平均、青い線が指数移動平均、水色の線が加重移動平均である。（全て20日）

反応の速さは加重移動平均＞指数移動平均＞単純移動平均 となっている。

単純移動平均では反応が悪い、と感じる場合には指数移動平均を利用すると良い。

また、移動平均線がレジスタンスラインやサポートラインになっている思われる箇所を図内に矢印で示した。

レジスタンスラインやサポートラインとして、加重移動平均がほとんど役に立っていないのに対し、単純移動平均以上に指数移動平均が機能しているようである。

この性質を利用したトレード方法に「指数移動平均線が上向きの際には移動平均線近くで買い、下向きの際には移動平均近くで売る」というものがある。 ※最後に紹介している「投資苑」という書籍で紹介されているトレーディングルールである。

＜参考書籍＞投資苑 (当サイトで省略したEMAの計算式も紹介されている)